音楽理論3 一覧に戻る

2021年6月 2日

3:Harmonizing実践①

Contents

実践 Harmonizing 練習曲

【3-2 Etude1】から

2小節目のE7altにあるメロディがこの楽曲で一番難しいハーモナイズになるので最後に説明します。
まずは3小節目からハーモナイズしていきます。
3小節目から5小節目の頭までメロディにインターバルを付けます。
最初に行うことはメロディをセンタートーン(Ct)とアプローチトーン(Ap)に分ける「メロディの仕分け」です。

ハモりをつけるメロディーの例

大事なことは、分数コードのときに「True Bass」を見抜くということです。
ダブルストラクチャーコード「Dm7/G」は本来「G7sus4(9)」です。
すなわちTrueBass=「G」です。
一方「E7alt/G♯」はインバージョンコードでベースが一時的にコードトーンのG♯を奏でているにすぎないのでTrue Bass=「E」です。

詳細に見ていきましょう。

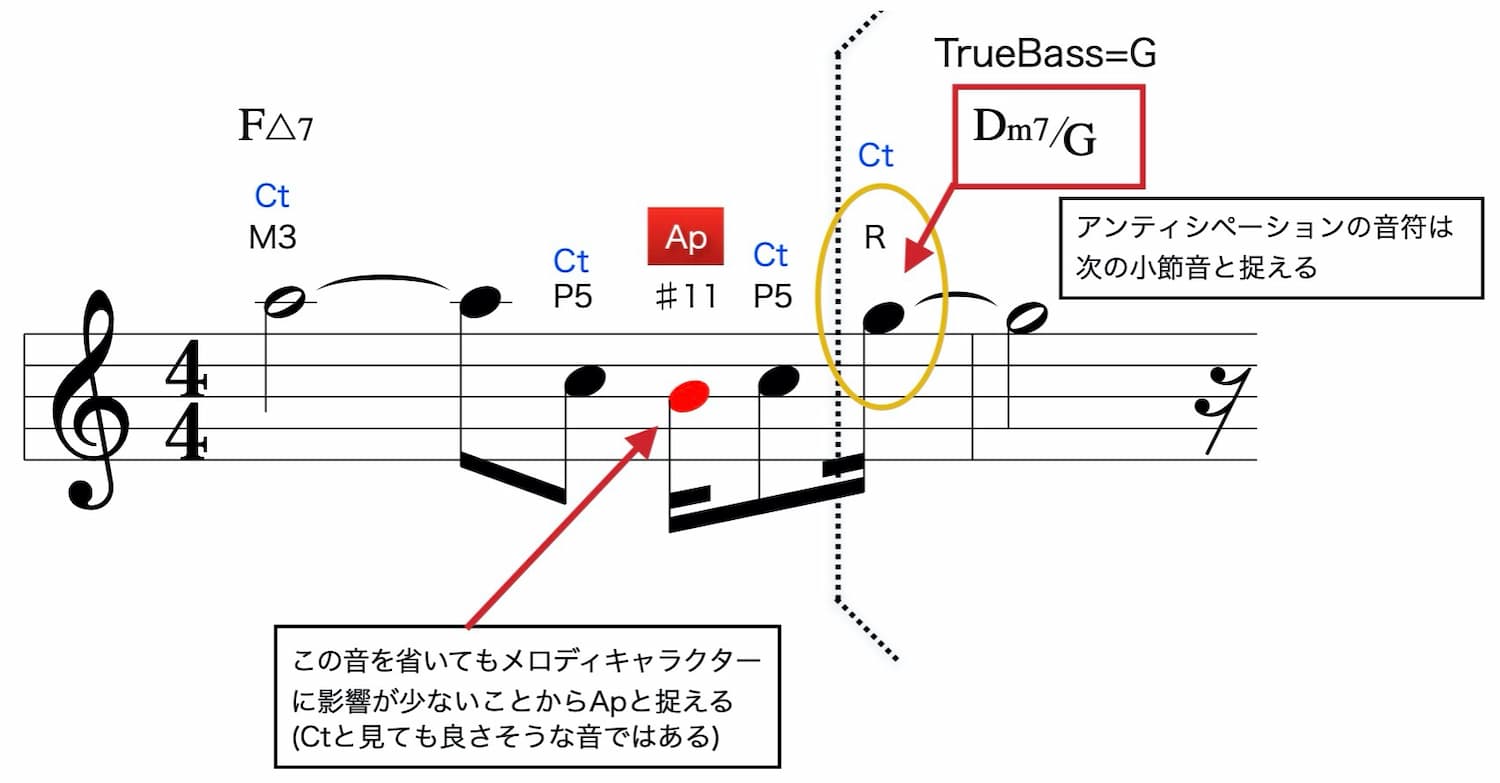
省いてもメロディのキャラクターへの影響が少ない音はアプローチトーンとして捉える　小節をまたぐアンティシペーションの音符は次の小節の音と捉える

「B=♯11」はCtともApとも取れそうです。
こんなときは「その音を省いてみる」という判別法があります。
Apならばメロディのキャラクターに大きな影響を与えません。
Ctならばメロディの本質が変わってしまいます。
この場合はApです。
最後の音「G」はアンティシペーションで次の小節をまたいでいます。
この時「概ね４分音符未満の音は次の小節に含まれる音として捉える」とするのが基本です。

次の部分。
ApはCtに「上下半音またはスケール上の全音」で解決しなければなりません。
よって「E→A→C」の部分は全てCtと捉えなければなりません。
また本来がsus4コードなので、「B=M3」がアボイド扱いとなりAp確定となります。

sus4コードでのM3はアプローチトーンとして解釈する　解決の定義を満たしていない音はセンタートーンとして捉える

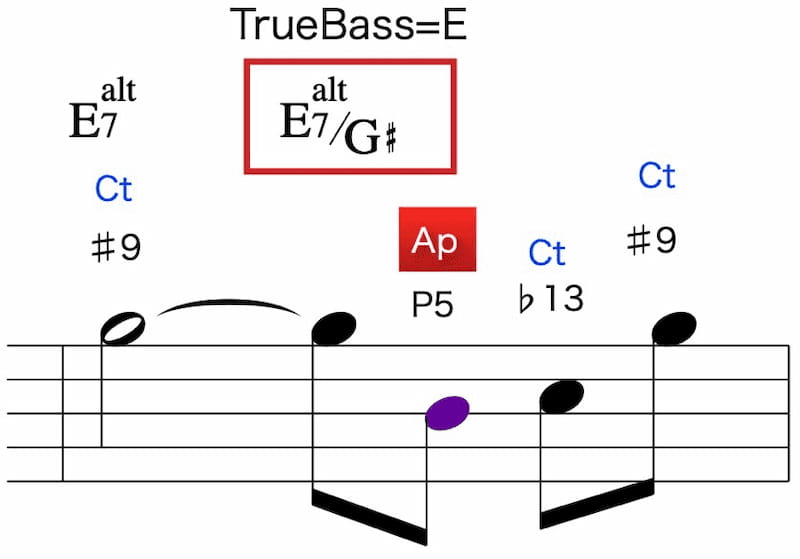
「E7alt」→「E7alt/G♯」
この部分はTrue Bass=EなのでAltered scale外の「B=P5」がApになります。

真のベース音(True bass)に基づいてアプローチトーンのインターバルを把握するオルタードドミナントにおけるP5はアプローチトーンとして扱う

ここまでの「メロディの仕分け」は次のようになります。

アプローチトーンとセンタートーンの仕分けが終わった状態

Ctを元コードでハーモナイズ

まずはCtに対して元コードでHarmonizingします。

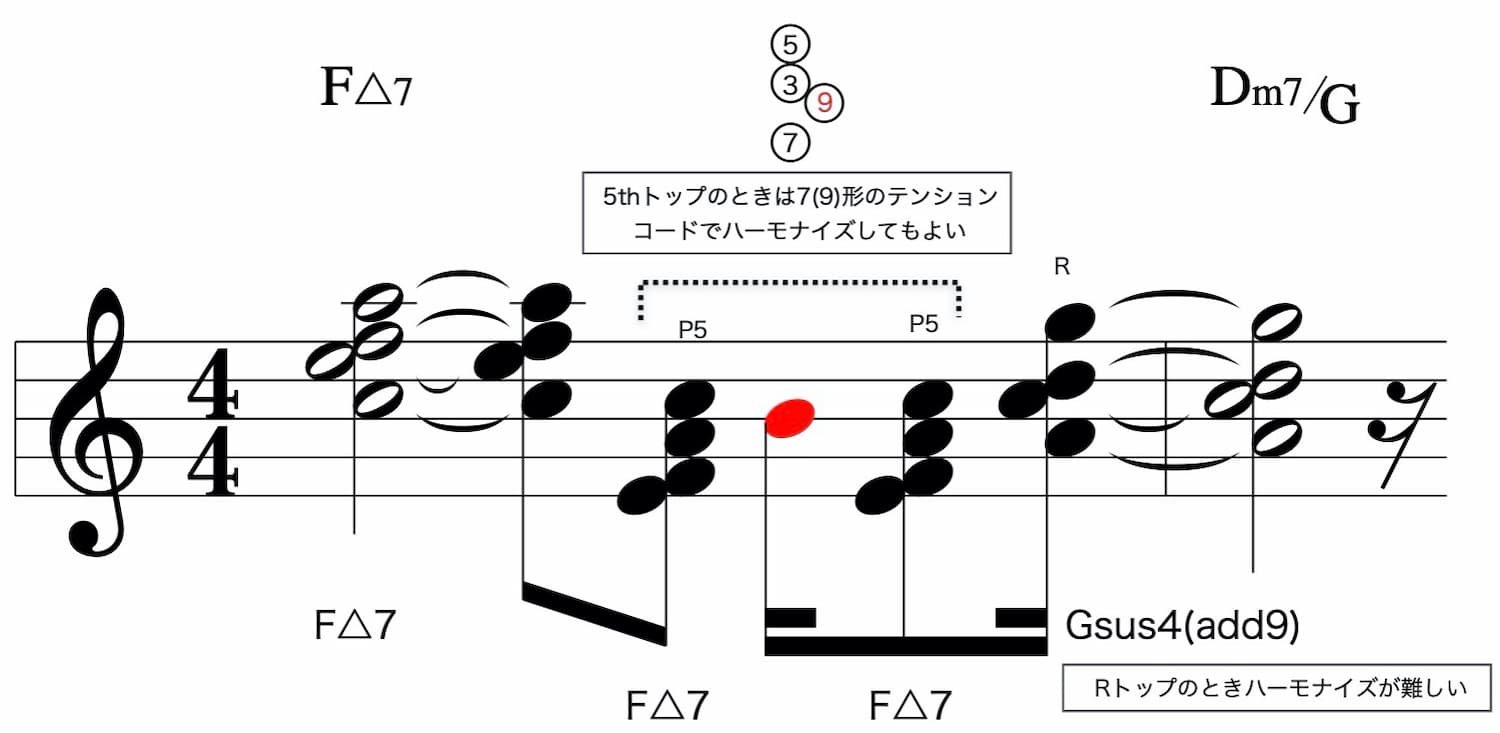
トップノートが5thになる場合、7(9)型のテンションコードでハーモナイズしてもよい　Rトップのときはハーモナイズが難しい

【Tips】5thメロのハーモナイズ
5thトップの場合はテンションコード形「7(9)」が使えます。
内部に(9)を持つ形でハーモナイズできます。
これは求めるサウンドの好みで選択して構いません。

Rメロのハーモナイズは難しい
Dm7/GのRメロ「G」は4和音でハーモナイズするのに悩む部分です。
Gから下オクターブ範囲でDm7の構成音は「F」「D」「C」とありますが、このまま全て使うと「C D F G」とクラスターコードになってしまいます。
そこで「F」を省き、あと一音足すのに「A」を加えます。

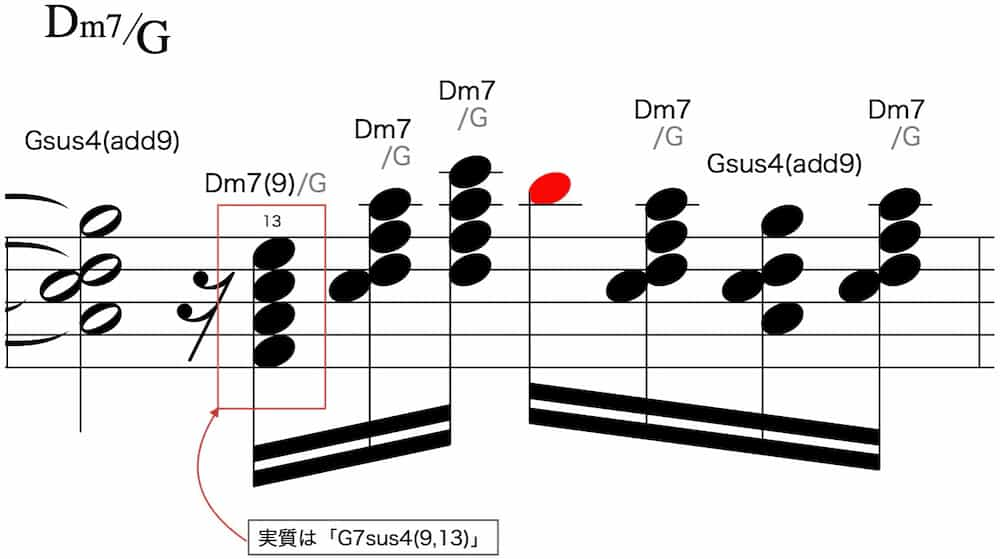
本来のコードは「G7sus4(9)」ですが、実践でのハーモナイズは分子部分の「Dm7」を考えれば良いことがわかります。
すると「E=13」はDm7(9)でハーモナイズすれば良いことになります。
Altered scaleでの元コードハーモナイズは「＋7」「7(♭5)」「7(♯9♭13)」「7(♭9♭13)」と多岐にわたります。
状況に応じて使い分けられることが必要です。
「C＝♭13」のところは「7(♯9♭13)」「7(♭9♭13)」の両方使用可能なところです。
これも実際に聴き比べて選択します。

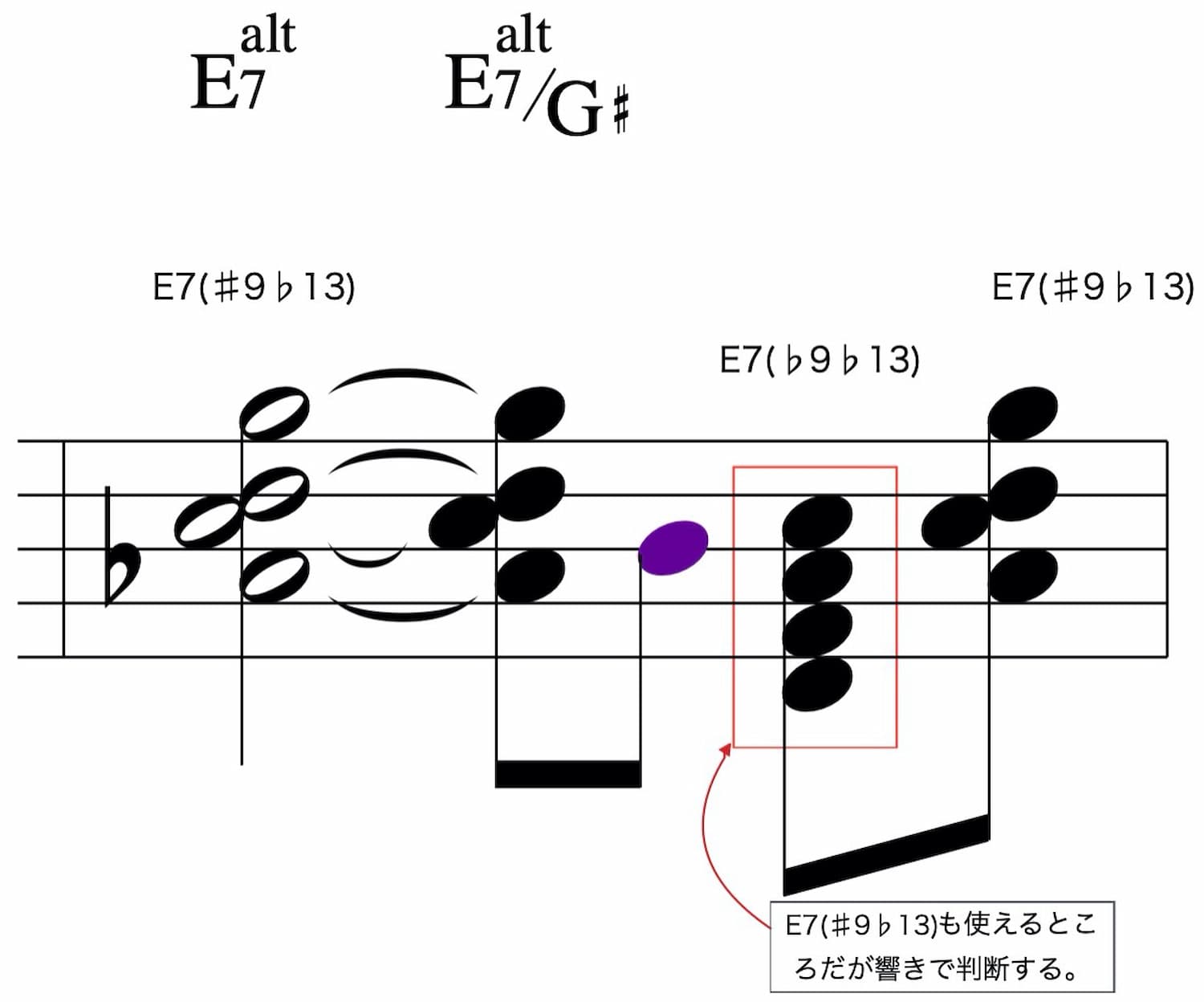
Apのアプローチコードを考える

音楽理論③第1回のアプローチコードの探し方チャートより「B=♯11」はSTAを選択します。
F△7はD7Cの「IV」なので「III=Em7」と「V=G6」がアプローチコードとなり、実質同じアプローチコードになります。
次の「B=M3」もSTAとなり、Dm7/GがD7Cの「V」なので「IV=F△7」「VI＝Am7」がアプローチコードとなります。
この場合「B」はF△7の♯11、Am7の9にあたるのでテンションコード形「F△7(9♯11)」「Am7(9)」を使いますが、結果は同じになります。

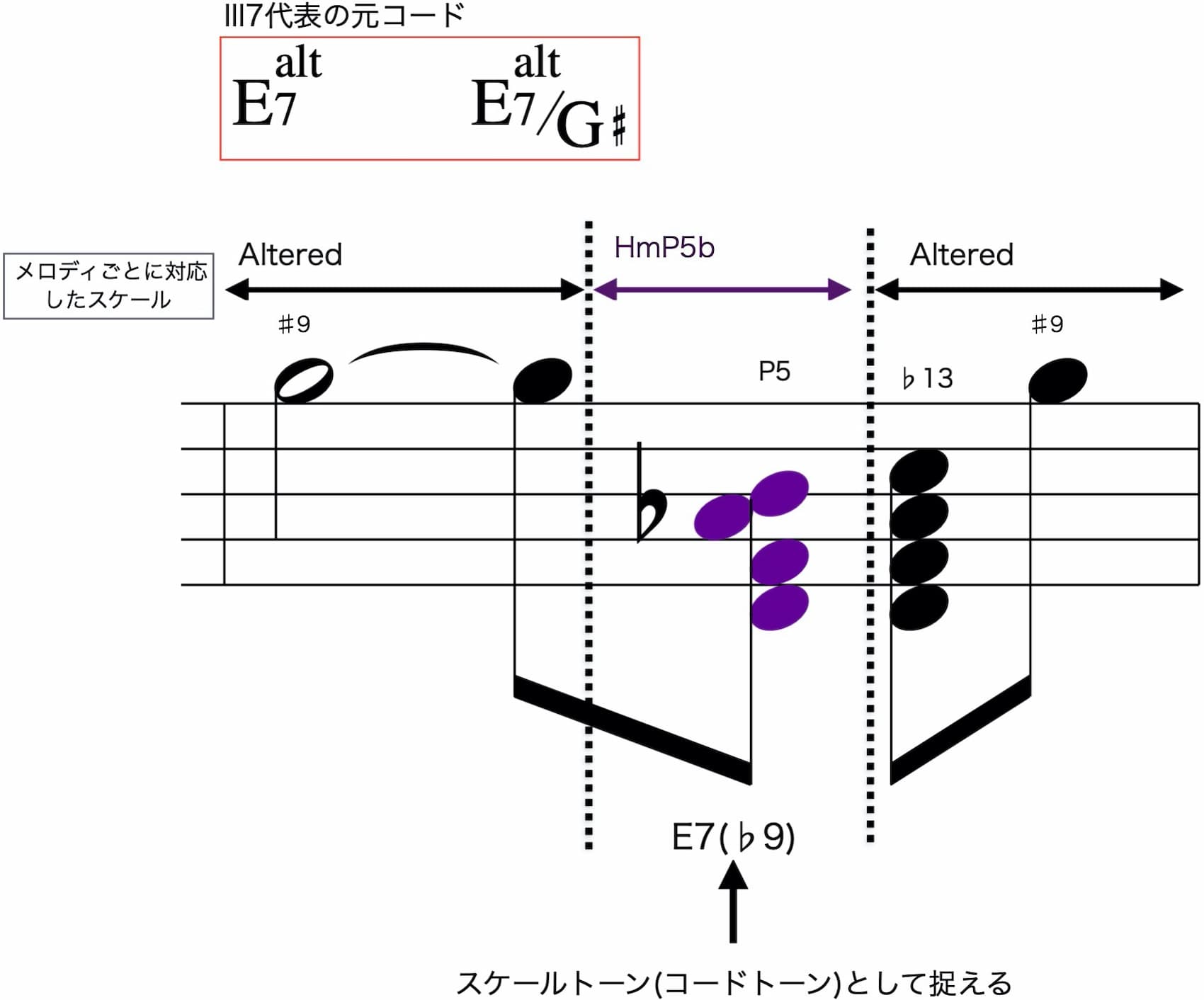
【重要】III7でのアプローチコード

E7altでの「B=P5」はスケール外の音であり、チャートからはCh.Aしかできません。
それに従って「D♯7(♭9♭13)」をアプローチコードとすると、サウンドに大きな違和感が発生します。
III７のときには、考え方を変えてハーモナイズに臨むことが求められます。

「III7のときはスケールが重ね合わせの状態になっている」

音楽理論①第12回の授業でIII7について学んだときに、III7のポジションには様々なスケールが対応することを説明しました。
アプローチハーモナイズにてIII7のときには

「メロディの1音づつにIII7対応スケールが変化していて、
その代表として元コードが付けられている」

と見ます。
実践ではほぼブロックコードによるハーモナイズになります。

「B=P5」の鳴っている時間内はHarmonic minor P5th belowが対応すると考えます。
するとHmP5bの対応コード「E7(♭9)」でハーモナイズできます。

III7は対応スケールの重ね合わせ状態になっている　アプローチコードは類型のコードによるブロックコードを選択する

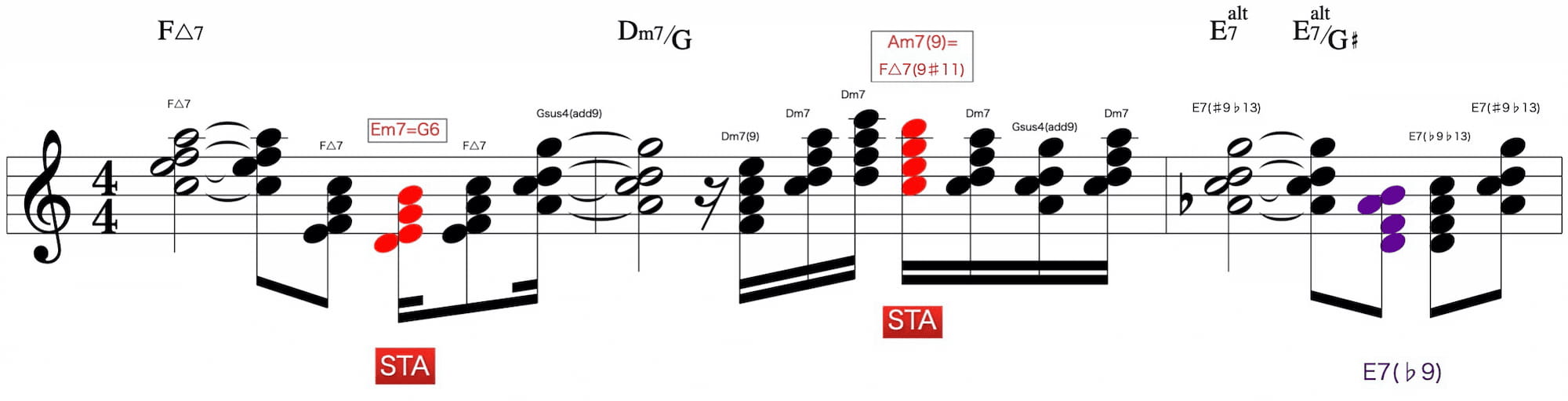
以上の説明から、ここまでのHarmonizingは次のようになります。

スケールトーンアプローチとブロックコードによるハモりの付け方の例

スケール別に見た全Approach Harmonizing

スケール別に全ての「ApからCtへの解決」をまとめることは、実践でアプローチハーモナイズを使いこなすのにとても有効です。
また、メロディの考察にもっとも威力を発揮します。
膨大な数になりますが確実に一つずつこなしていきましょう。
まずはCtを決めて、できうるApを全て考え、アプローチハーモナイズを書き記していきます。
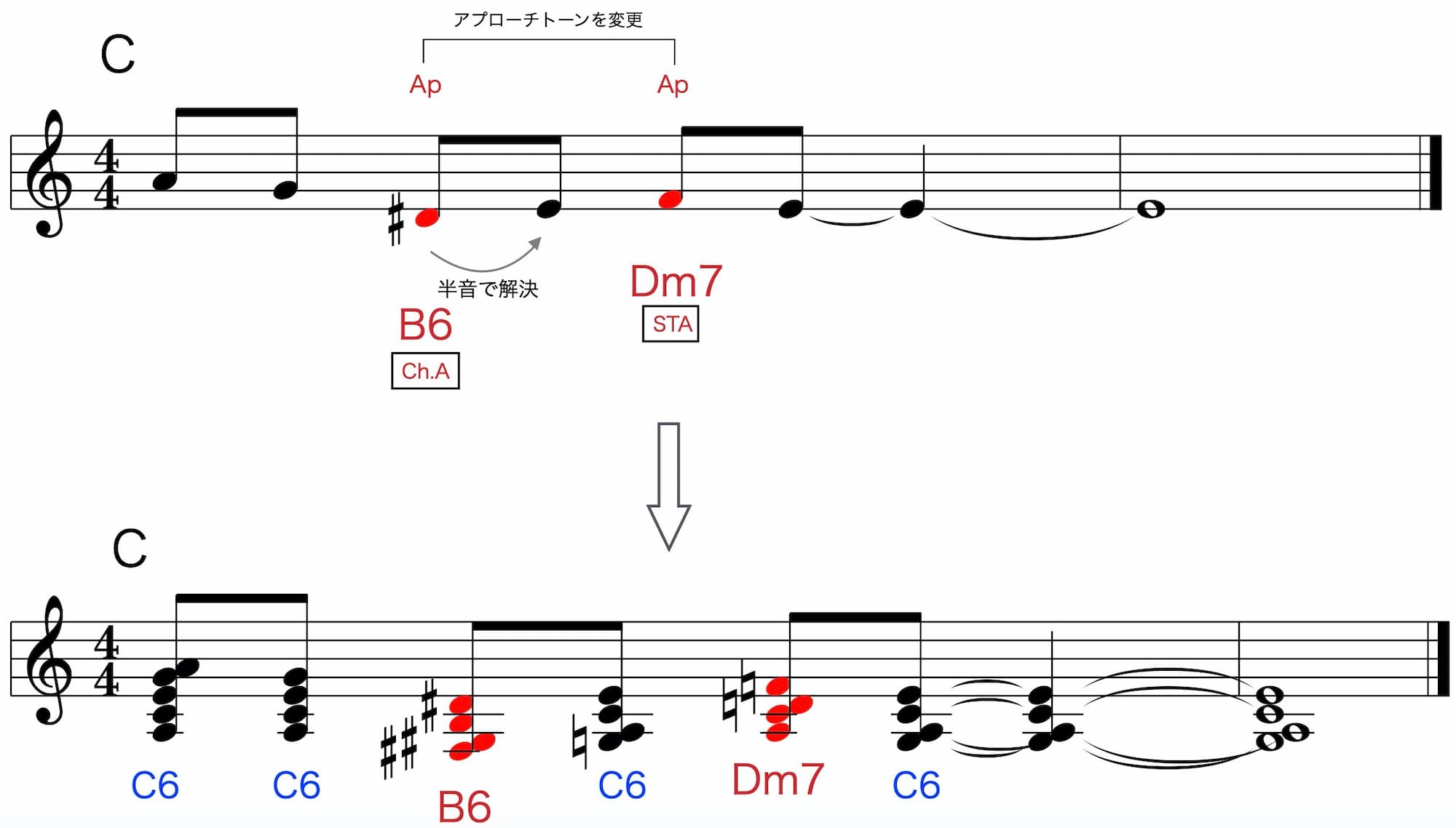
便宜上：Cにて進めます。

Ionianでの全Approach Harmonizing

元コード=C6 Ct＝E(M3)の時

ハモりの付け方の例・クロマチックアプローチとスケールトーンアプローチ