9:4度堆積②

4度堆積コードからスケールを考察する②

P4の堆積数を増やすごとに、対応できるスケールが減少していきます。
順を追ってみていきましょう。

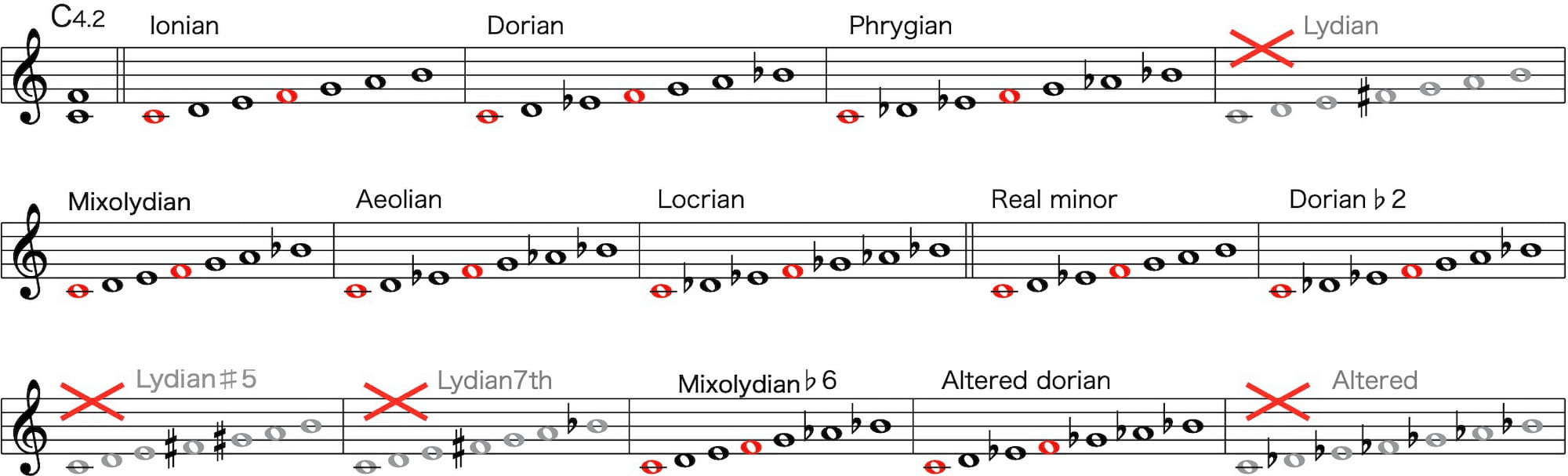
C4.2
11thが積まれます。
よって♯11を持つLydian系3本とAlteredが消えます。

C4.3
m7が積まれます。
よってM7を持つIonianとReal minorが消えます。

C4.4
m3が積まれます。
よってM3を持つMixolydianとMixolydian♭6が消えます。

C4.5
♭13が積まれます。
よって13を持つDorianとDorian♭2が消えます。

C4.6
♭9が積まれます。
よって9thを持つAeolianとAltered dorianが消えます。

C4.7
o5が積まれます。
P5のPhrygianが消えて、最後にLocrianが残ります。

通常の3度堆積では、重要スケールだったIonian、Lydianなどが早々と消えたのに対し、4度堆積では、さほど重要では無かったLocrianが最後まで残るところに、音楽の面白さが現れているといえるでしょう。

通常システムへの4度堆積の流用

通常のコード＆スケールシステムに、4度堆積を流用する方法を考えてみます。
C4.3をP4パーツとした上部和音構造と捉えた時に、どんなルートでコードを再構築できるかを見てみます。
低音パートにてコード構成を補完させています。

「特殊」とあるのは、発展的なコード構造となったものです。
唯一、Bをルートとした場合のみC-B-B♭と半音が連続するため、コードを再構築できません。
特に汎用性の高いコードは赤く囲ってあります。

【3-9 Etude1】
これらのコードを用いた参考曲です。
各コード対応のスケールに留意してください。

Major scale
systemに置き換えてみる

4度堆積によるスケール考察にて、最後まで残ったものがLocrianでした。
ならばB4.3をP4パーツとした時に、Key of CのDiatonic上にて使えるコード群が導き出せるはずです。

【3-9 Etude2】
Key of Cにての参考曲です。